Microwave Discrete and Microstrip Filter Design

Theory, Design Methodology, Microwave filters are two-port networks that select desired frequency bands (passband) and suppress unwanted frequency bands (stopband). They are essential for signal clarity in commercial (5G, satellite) and military (radar) systems

1. Introduction

“Microwave filters are reactive two-port networks designed to pass signals within a desired frequency range while attenuating unwanted components.”

Modern RF and microwave systems such as wireless communication links, radar, satellite payloads, and sensing platforms require high-performance filters to ensure spectral purity and system stability. Unlike low-frequency filters, microwave filters must account for distributed effects, discontinuities, and electromagnetic coupling. Therefore, their design combines circuit theory, transmission-line concepts, and full-wave electromagnetic simulation.

2. Microwave filters are fundamental components in RF and microwave

Microwave filters are fundamental components in RF and microwave front ends, used to suppress out-of-band signals. They are classified as:

LPF

Low-Pass Filter

Passes frequencies below the cutoff frequency $f_{c}$.

HPF

High-Pass Filter

Passes frequencies above the cutoff frequency $f_{c}$.

BPF

Band-Pass Filter

Passes frequencies between $f_{1}$ and $f_{2}$.

BSF

Band-Stop / Notch Filter

Rejects frequencies between $f_{1}$ and $f_{2}$.

3. General Design Procedure

The design of a microwave filter generally involves the following steps:

Specifications: Define the desired frequency response (passband, stopband, insertion loss, ripple, and return loss).
Low-Pass Prototype: Design a normalized low-pass prototype ($g$ values) for a cutoff frequency of $\Omega_c = 1 \text{ rad/s}$ and an impedance of $1 \Omega$.
Frequency and Impedance Scaling: Scale the prototype to the desired cutoff frequency ($f_c$) and characteristic impedance ($Z_0$).
Filter Transformation: If required, transform the low-pass prototype into a high-pass, band-pass, or band-stop filter.
Realization: Convert the lumped $L$ and $C$ elements into distributed elements (microstrip lines, stubs, or coupled lines).
Simulation and Optimization: Use software like Keysight ADS to verify and optimize the design.

Filter Response & Circuit Graphics

LOW-PASS RESPONSE

HIGH-PASS RESPONSE

BAND-PASS RESPONSE

BAND-STOP RESPONSE

Comparison of Approximation Functions

Figure: Steeper roll-off of Chebyshev vs Maximally Flat Butterworth response.

4. Filter Synthesis Methods

Image Parameter Method: Older technique based on image impedances; offers limited control and is rarely used in modern design.

Insertion Loss Method: Most widely used synthesis technique. Based on network theory and polynomial approximations (Butterworth, Chebyshev, Elliptic). It is the standard implemented in ADS.

Numerical Synthesis: Relies on full-wave EM optimization. Highly accurate but computationally intensive; used for fine tuning and novel structures.

5. Approximation Functions

Type	Characteristic	Best For
Butterworth	Maximally flat passband, monotonic response.	Smooth amplitude response.
Chebyshev	Equiripple in passband, sharper cutoff.	High selectivity, lower order.
Bessel	Linear phase response, poor selectivity.	Waveform/Pulse preservation.
Elliptic	Ripple in both bands, sharpest transition.	Very high rejection, compact size.

6. Order Calculation ($N$)

Butterworth Approximation

$$L_{A}(\omega^{\prime})=10 \log_{10}[1+\epsilon^{2}(\frac{\omega^{\prime}}{\omega_{c}})^{2N}]$$ Where \(\epsilon = \sqrt{10^{L_A/10}-1}\)

Chebyshev Approximation (Stopband Region $\omega^{\prime} \ge \omega_1^{\prime}$)

L_{A}(\omega^{\prime})=10 \log_{10}[1+\epsilon^{2}\cosh^{2}(N \cosh^{-1}(\frac{\omega^{\prime}}{\omega_{1}^{\prime}}))]

7. Prototype Values ($g_k$)

Butterworth Prototype

g_{k}=2 \sin\left(\frac{(2k-1)\pi}{2n}\right), \quad k=1,2,…,n$$ $$g_0 = 1, \quad g_{n+1} = 1

Chebyshev Prototype Parameters

\beta=\ln[\coth(\frac{L_{Ar}}{17.37})], \quad \gamma=\sinh(\frac{\beta}{2n})$$ $$a_{k}=\sin(\frac{(2k-1)\pi}{2n}), \quad b_{k}=\gamma^{2}+\sin^{2}(\frac{k\pi}{n})$$ $$g_{1}=\frac{2a_{1}}{\gamma}, \quad g_{k}=\frac{4a_{k-1}a_{k}}{b_{k-1}g_{k-1}}

Note: For Chebyshev $g_{n+1}$: If $n$ is odd, $g_{n+1}=1$. If $n$ is even, $g_{n+1}=\coth^2(\frac{\beta}{4})$.

8. Frequency and Impedance Scaling

For Low-Pass Filters:

C_{k}^{\prime}=\frac{C_{k}}{R_{0}\omega_{c}}

L_{k}^{\prime}=\frac{R_{0}L_{k}}{\omega_{c}}

For Band-Pass Filters:

Transformation into resonant LC circuits where $\Delta = \frac{\omega_2 – \omega_1}{\omega_0}$:

L_{1}^{\prime}=\frac{L_{1}Z_{0}}{\omega_{0}\Delta}, \quad C_{1}^{\prime}=\frac{\Delta}{L_{1}Z_{0}\omega_{0}}$$ $$L_{2}^{\prime}=\frac{\Delta Z_{0}}{\omega_{0}C_{2}}, \quad C_{2}^{\prime}=\frac{C_{2}}{\omega_{0}Z_{0}\Delta}

9. Distributed Realization

In microwave implementations, lumped inductors and capacitors are replaced by high- and low-impedance transmission-line sections.

Electrical Length Formulas:

\beta l_{c}=\frac{C_{k}Z_{l}}{R_{0}}, \quad \beta l_{l}=\frac{L_{k}R_{0}}{Z_{h}}

Calculated Physical Lengths (Example $f_c=2$ GHz):

// Design Values for Zl=10 Ω, Zh=100 Ω

βl_c1 = 0.1530, βl_l2 = 0.9239

βl_c3 = 0.3695, βl_l4 = 0.3827

// Resulting Dimensions (Physical Lengths)

l_c1: 1.680 mm

l_l2: 10.145 mm

l_c3: 4.057 mm

l_l4: 4.202 mm

10. ADS Simulation Design Steps

Setup Workspace

Launch Keysight ADS, create a new workspace, and open a new schematic window.

Lumped Component Placement

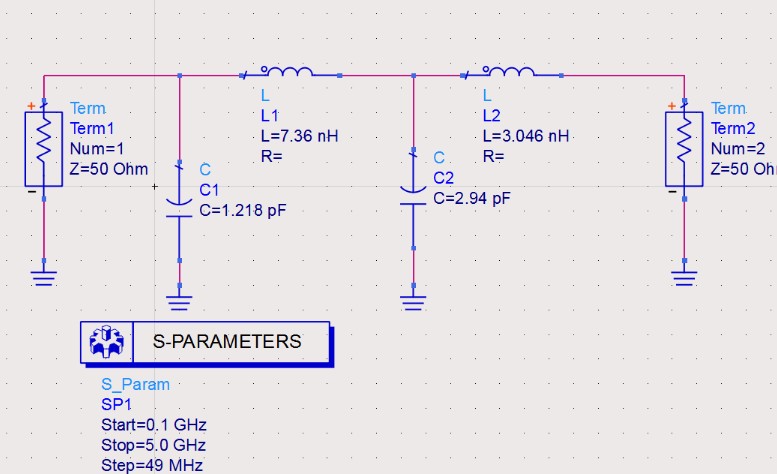
Select L and C from the Lumped-Components library. Arrange components according to low-pass topology.

Component Parameterization

Enter calculated values: $C_1=1.218\text{pF}$, $L_2=7.35\text{nH}$, $C_3=2.94\text{pF}$, $L_4=3.046\text{nH}$.

Simulation & Verification

Perform S-parameter simulation to observe attenuation and verify that requirements are met.

Microwave Discrete and Microstrip Filter Design

Microwave Discrete and Microstrip Filter Design

1. Introduction

2. Microwave filters are fundamental components in RF and microwave

Low-Pass Filter

High-Pass Filter

Band-Pass Filter

Band-Stop / Notch Filter

3. General Design Procedure

Filter Response & Circuit Graphics

LOW-PASS RESPONSE

HIGH-PASS RESPONSE

BAND-PASS RESPONSE

BAND-STOP RESPONSE

Comparison of Approximation Functions

4. Filter Synthesis Methods

5. Approximation Functions

6. Order Calculation (\(N\))

Butterworth Approximation

Chebyshev Approximation (Stopband Region \(\omega^{\prime} \ge \omega_1^{\prime}\))

7. Prototype Values (\(g_k\))

Butterworth Prototype

Chebyshev Prototype Parameters

8. Frequency and Impedance Scaling

For Low-Pass Filters:

For Band-Pass Filters:

9. Distributed Realization

Electrical Length Formulas:

Calculated Physical Lengths (Example \(f_c=2\) GHz):

10. ADS Simulation Design Steps

Setup Workspace

Lumped Component Placement

Component Parameterization

Simulation & Verification

Microwave Schematic Reference Fig

Leave a Comment Cancel Reply

Contact

Company

Subscribe Now